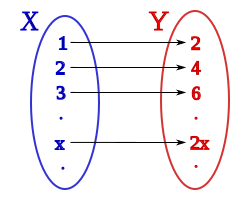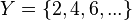terremotos - videos educativos.flv

FUNCIONES REALES

Ejemplo

en el diagrama de la figura:

todos los elementos de Y, que tienen origen, tienen un único origen, esto hace que la aplicación sea inyectiva

todos los elementos de Y, tienen origen, esto hace que la aplicación sea sobreyectiva.

Si tomaremos por conjunto inicial el conjunto de los números naturales:

y por conjunto final el de los números naturales pares:

Podemos ver que la relación

Por el que a cada número natural x de X, le asociamos un número par 2x de Y, se cumple:

1. f: es una aplicación, dado que a cada uno de los valores x de X le corresponde un único valor 2x de Y.
2. esta aplicación es inyectiva dado que a cada número par 2x de Y le corresponde un único valor x de X.
3. y es sobreyectiva porque todos los números pares tienen un origen

Esto nos permite afirmar que hay el mismo número de números naturales que de números naturales pares, se da la paradoja de que los números naturales pares en un subconjunto propio de los números naturales, esta circunstancia solo se da con los conjuntos infinitos.
En el siguiente ejemplo podemos observar  que el conjunto de parejas ordenadas en el cual los elementos de Y tienen su propio origen miramos que todos los elementos se unen para formar un solo conjunto en donde los elementos de X  se dirigen hacia los elementos de Y. bueno esto fue lo que yo comprendi de las funcines reales espero que le guste adios..

LA TECNOLOGÍA DE INFORMACIÓN Y COMUNICACIÓN EN LA EDUCACIÓN

Documento escrito en word. ver pantalla completa


La Tecnología De Información y Comunicación En La Educación